关于Transformer网络结构,最早是发布在论文《Attention Is All You Need》。已经有不少人对该论文进行了详细的解读,而这里是从一个小白的角度进行介绍。
实话说,第一次接触Transformer的网络结构,完全是看不懂的。毕竟没有基础,直到对CV有了一定的了解后回过头来再看Transformer一下子就通了。其网络结构图如下:
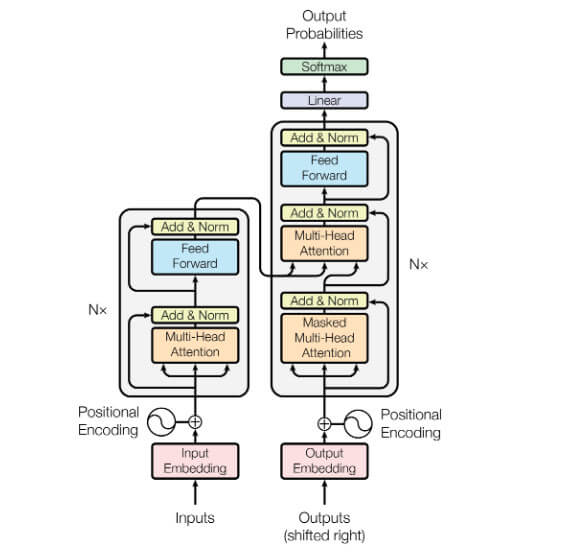
其中左侧部分为Encoder,而右侧为Decoder结构。其中Inputs代表输入,经过嵌入后与位置编码拼接在一起传入到Encoder中。
整个Encoder由4部分结构组成:
- 多头注意力结构-Multi-Head Attention
- 前馈结构-Feed Forward
- 残差连接-residual connection
- LN结构-Layer Normalization
我们对之前的网络结构图进行标注后有:
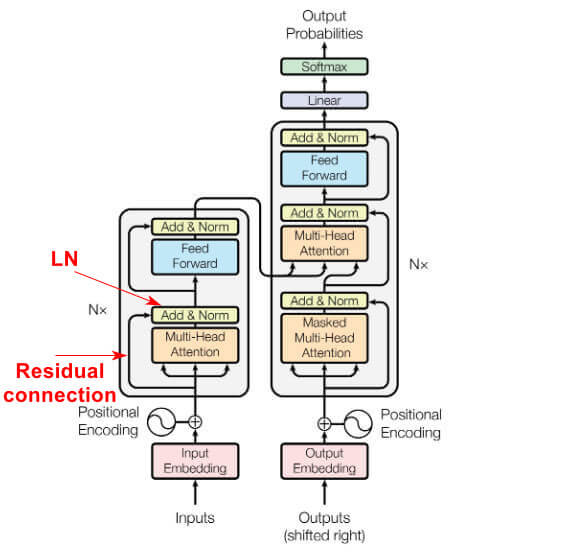
其中输入中有一条路径直接不经过Multi-Head Attention直接到达Add & Norm,而这条路径就是残差连接,其源自残差网络(Residual Network,ResNet)。而之后的Norm是LN层。
在Encoder中Nx表示有N个这样的网络结构。继续沿着这条路径,可以发现Decoder中也有类似的网络结构。但是在Decoder中前面还有1个Masked Multi-Head Attention与Add & Norm层。此时看Transformer网络结构是不是就很简单了。
另外在Transformer中很喜欢说的注意力机制,常常会使用Q,K,V这3个向量容易让人摸不着头脑。此时只要记住这样一个事情,注意力机制的主要目的是将查询与一组键值对进行比较,并计算出查询与每个键之间的相关性得分,然后使用这些得分对值进行加权平均。
而打分函数主要有点积和加性两种操作,一般都是采用前者。此时就可以理解其公式了:
$$ \text{Score}(Q,K)=QK^{T} $$
之后再经过归一化操作
$$ \text{Softmax}(\text{Score})=\frac{e^{\text{score}}}{\sum e^{\text{score}}} $$
将其与值相乘进行加权平均就得到了注意力矩阵了$$ \text{Attention}(Q,K,V)=\sum(\text{Softmax}(\text{Score})\cdot V) $$
其中归一化使用的是Softmax函数。是不是很简单,网上很多文章写得让人看着云里雾里的。
整个过程可以说非常简单,首先计算出相关性矩阵,之后对这个相关性矩阵再乘以一个值的权重矩阵从而对这些相关性有一个重要性的区分。这就是所谓的注意力机制了,对于某些部分关注很高,而某些部分则选择性遗忘。

